Student Question: Misconceptions are often regarded as “mistakes”.
- Give FIVE examples of misconceptions that learners might have relating to quadratic equations.
- Discuss how you will help a learner to remedy the misconceptions that you identified.
Misconceptions Related to Quadratic Equations:
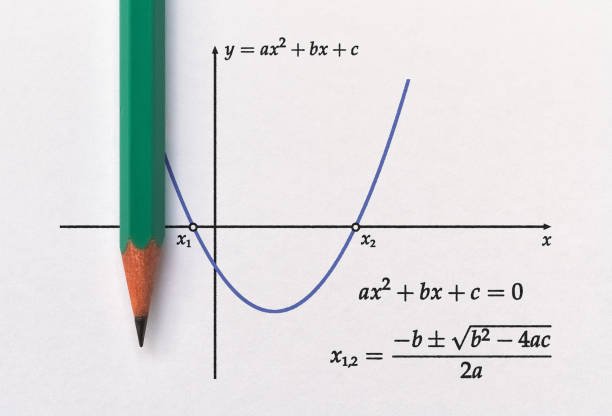
Intercepts: Belief that a quadratic always intersects the x-axis twice.
Solution: Clarify that quadratics can have two, one, or no real x-intercepts depending on the discriminant.
Graph Shape: Assuming all quadratic graphs are upward-facing parabolas.
Solution: Explain the role of the leading coefficient and introduce both upward and downward-facing parabolas.
Factorization: Thinking every quadratic can be factored over the integers.
Solution: Introduce the quadratic formula and the concept of irrational and complex solutions.
Vertex: Misunderstanding that the vertex is always the highest or lowest point.
Solution: Differentiate between maximum and minimum vertex points based on the leading coefficient’s sign.
Roots: Confusing real roots with imaginary roots.
Solution: Elaborate on the discriminant’s role in determining the nature of the roots.
By addressing these misconceptions with clear explanations and visual aids, educators can help learners build a solid understanding of quadratic equations.
FIVE Examples of Misconceptions that Learners Might Have Relating to Quadratic Equations
Intercepts:
Misconception: Some learners believe that every quadratic equation will always intersect the x-axis twice. This misconception might arise because many of the initial examples students encounter have two distinct x-intercepts.
Solution: It’s crucial to explain the concept of the discriminant (b² – 4ac) in the quadratic formula. The discriminant determines the nature of the roots. If it’s positive, the quadratic has two distinct real roots. If it’s zero, there’s one real root (or a repeated root). If it’s negative, there are no real roots, leading to complex or imaginary solutions. Using graphical representations to show the different possibilities can further enhance understanding.
Graph Shape:
Misconception: Students often assume all quadratic graphs are upward-facing parabolas, especially if they’ve mainly seen positive leading coefficients.
Solution: The direction in which the parabola opens is determined by the leading coefficient. If it’s positive, the parabola opens upwards, and if it’s negative, it opens downwards. Visual demonstrations using graph plotting tools and varying coefficients can help students visualize and understand this concept better.
Factorization:
Misconception: A common misconception is thinking that every quadratic equation can be factored over the integers. While many quadratic equations taught in early algebra can be factored easily, not all can.
Solution: Introduce students to the quadratic formula, which can solve any quadratic equation. Explain that while some quadratics have nice, integer factors, others may have irrational or even complex roots. Practice with a variety of examples can help cement this understanding.
Vertex:
Misconception: Students sometimes believe that the vertex of a quadratic graph is always its highest point or always its lowest point, without considering the parabola’s direction.
Solution: It’s essential to highlight that the vertex is the maximum point when the parabola opens downward and the minimum when it opens upward. This can be tied back to the leading coefficient’s sign. Using tools to graphically represent parabolas and point out the vertex can be beneficial.
Roots:
Misconception: There’s a tendency to confuse real roots with imaginary roots, especially when learners first encounter complex numbers.
Solution: As with the first misconception, the discriminant plays a vital role. Educators should emphasize that a negative discriminant results in complex or imaginary roots, and these don’t intersect the x-axis on a standard real number plane. Using the quadratic formula to solve a variety of equations can give students the practice they need to differentiate between real and imaginary roots.